【初中数学】几何经典难题(二)附答案解析
 2022-05-07
2022-05-07 
 iXueHai.cn
iXueHai.cn
 爱学海
字体 - 小
+ 大 纠错指正
爱学海
字体 - 小
+ 大 纠错指正
|
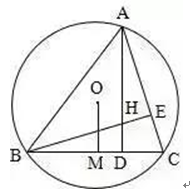
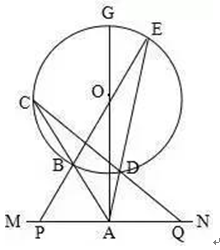
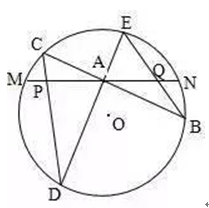
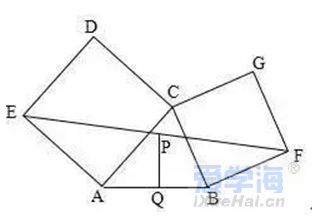
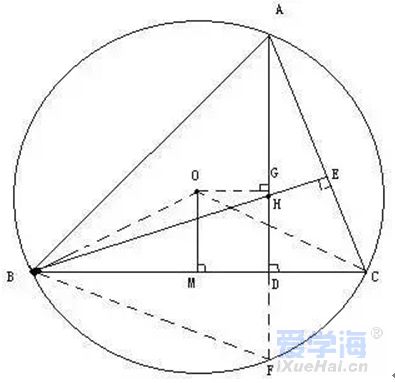
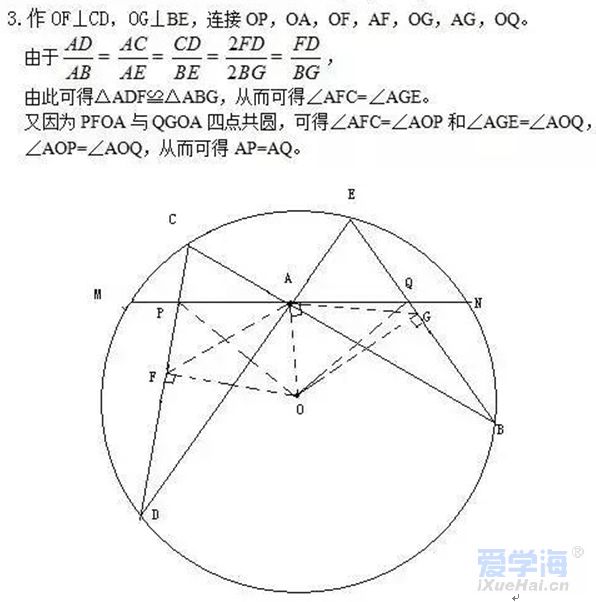
1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M. (1)求证:AH=2OM; (2)若∠BAC=600,求证:AH=AO. 2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q. 求证:AP=AQ. 3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题: 设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q. 求证:AP=AQ. 4、如图,分别以△ABC的AC和BC为一边,在△ABC的外侧作正方形ACDE和正方形CBFG,点P是EF的中点. 求证:点P到边AB的距离等于AB的一半. 答案解析 1. (1)延长AD到F连BF,做OG⊥AF, 又∠F=∠ACB=∠BHD, 可得BH=BF,从而可得HD=DF, 又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM (2)连接OB,OC,既得∠BOC=1200从而可得∠BOM=600, 所以可得OB=2OM=AH=AO,得证。 |
下一篇:【初中数学】几何经典难题(三)
本栏目热门阅读
本栏目最新文章
| 高三: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初三: 语文| 数学| 英语| 物理| 化学| 历史| 道德与法制 |
| 高二: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初二: 语文| 数学| 英语| 物理| 地理| 生物| 历史| 道法 |
| 高一: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初一: 语文| 数学| 英语| 物理| 地理| 生物| 历史| 道法 |
| 小学: 语文| 数学| 英语| 道德与法制| 科学| 试题: 小学| 初中| 中考| 高中| 高考| 作文: 小学| 初中| 高中| 满分| 技巧|素材|英汉词典 |
| 高校: 985/211| 各省市| 港澳台| 国外| 排名| 中考专辑| 高考专辑| 各省中学| 职业考试: 从业资格| 技术技能| 艺术等级| 公务员| 百年党史 |
| 课外: 教育动态| 教育法规| 老师榜| 家长帮| 学生派| 安全说| 古诗古文| 世界名著| 近代文学| 寓言故事| 格言名句| 阅读技巧| 在线许愿祝福 |
Copyright © 2019-2023 爱学海 ixuehai.cn 版权所有 | 关于爱学海 | 商标证书 | 投诉反馈 | 版权声明 | 公司简介 | 中采网 | 粤ICP备09029428号
 移动版
移动版