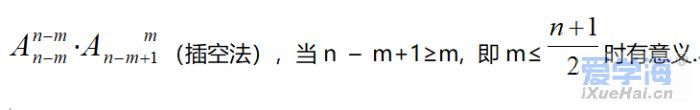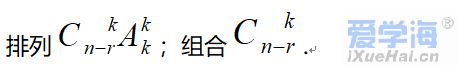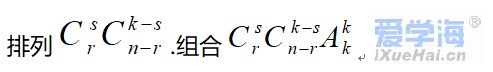【高中数学】第十章-排列组合二项定理 四、排列、组合综合
 2021-10-06
2021-10-06 
 iXueHai.cn
iXueHai.cn
 爱学海
字体 - 小
+ 大 纠错指正
爱学海
字体 - 小
+ 大 纠错指正
|
1. I. 排列、组合问题几大解题方法及题型: ①直接法. ②排除法. ③捆绑法:在特定要求的条件下,将几个相关元素当作一个元素来考虑,待整体排好之后再考虑它们“局部”的排列.它主要用于解决“元素相邻问题”,例如 ④插空法:先把一般元素排列好,然后把待定元素插排在它们之间或两端的空档中,此法主要解决“元素不相邻问题”. 例如:n个元素全排列,其中m个元素互不相邻,不同的排法种数为多少? ⑤占位法:从元素的特殊性上讲,对问题中的特殊元素应优先排列,然后再排其他一般元素;从位置的特殊性上讲,对问题中的特殊位置应优先考虑,然后再排其他剩余位置.即采用“先特殊后一般”的解题原则. ⑥调序法:当某些元素次序一定时,可用此法.解题方法是: 例如:n个元素全排列,其中m个元素顺序不变,共有多少种不同的排法? 解法一:(逐步插空法)(m+1)(m+2)…n = n!/ m!; 时有意义. ⑧隔板法:常用于解正整数解组数的问题. ⑩指定元素排列组合问题. 01. 从n个不同元素中每次取出k个不同的元素作排列(或组合),规定某r个元素都包含在内 。先C后A策略, 02. 从n个不同元素中每次取出k个不同元素作排列(或组合),规定某r个元素都不包含在内。先C后A策略, 从n个不同元素中每次取出k个不同元素作排列(或组合),规定每个排列(或组合)都只包含某r个元素中的s个元素。先C后A策略, 1. 排列组合常见解题策略: ①特殊元素优先安排策略; ②合理分类与准确分步策略; ③排列、组合混合问题先选后排的策略(处理排列组合综合性问题一般是先选元素,后排列); ④正难则反,等价转化策略; ⑤相邻问题插空处理策略; ⑥不相邻问题插空处理策略; ⑦定序问题除法处理策略; ⑧分排问题直排处理的策略; ⑨“小集团”排列问题中先整体后局部的策略; ⑩构造模型的策略. |
| 高三: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初三: 语文| 数学| 英语| 物理| 化学| 历史| 道德与法制 |
| 高二: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初二: 语文| 数学| 英语| 物理| 地理| 生物| 历史| 道法 |
| 高一: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初一: 语文| 数学| 英语| 物理| 地理| 生物| 历史| 道法 |
| 小学: 语文| 数学| 英语| 道德与法制| 科学| 试题: 小学| 初中| 中考| 高中| 高考| 作文: 小学| 初中| 高中| 满分| 技巧|素材|英汉词典 |
| 高校: 985/211| 各省市| 港澳台| 国外| 排名| 中考专辑| 高考专辑| 各省中学| 职业考试: 从业资格| 技术技能| 艺术等级| 公务员| 百年党史 |
| 课外: 教育动态| 教育法规| 老师榜| 家长帮| 学生派| 安全说| 古诗古文| 世界名著| 近代文学| 寓言故事| 格言名句| 阅读技巧| 在线许愿祝福 |
 移动版
移动版