【初中数学】BS版八年级上册 第四章 一次函数
 2021-10-20
2021-10-20 
 iXueHai.cn
iXueHai.cn
 爱学海
字体 - 小
+ 大 纠错指正
爱学海
字体 - 小
+ 大 纠错指正
|
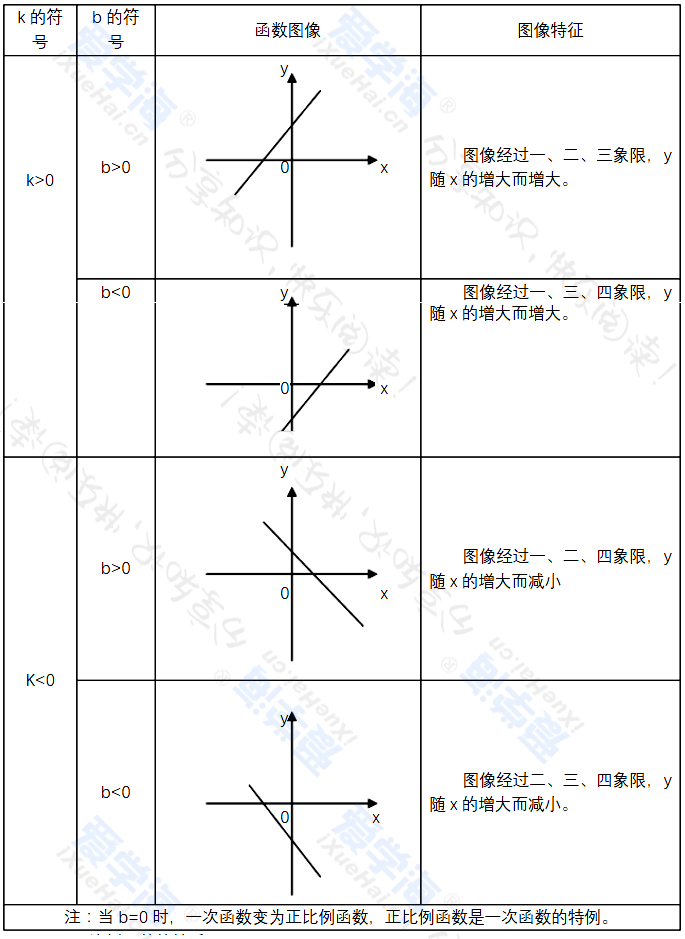
第四章 一次函数 一、函数: 一般地,在某一变化过程中有两个变量x与y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量。 二、自变量取值围 使函数有意义的自变量的取值的全体,叫做自变量的取值围。一般从整式(取全体实数),分式(分母不为0)、二次根式(被开方数为非负数)、实际意义几方面考虑。 三、函数的三种表示法及其优缺点 (1)关系式(解析)法 两个变量间的函数关系,有时可以用一个含有这两个变量及数字运算符号的等式表示,这种表示法叫做关系式(解析)法。 (2)列表法 把自变量x的一系列值和函数y的对应值列成一个表来表示函数关系,这种表示法叫做列表法。 (3)图象法 用图象表示函数关系的方法叫做图象法。 四、由函数关系式画其图像的一般步骤 (1)列表:列表给出自变量与函数的一些对应值 (2)描点:以表中每对对应值为坐标,在坐标平面描出相应的点 (3)连线:按照自变量由小到大的顺序,把所描各点用平滑的曲线连接起来。 五、正比例函数和一次函数 1、正比例函数和一次函数的概念 一般地,若两个变量x,y间的关系可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称y是x的一次函数(x为自变量,y为因变量)。 特别地,当一次函数y=kx+b中的b=0时(即y=kx)(k为常数,k≠0),称y是x的正比例函数。 2、一次函数的图像: 所有一次函数的图像都是一条直线 3、一次函数、正比例函数图像的主要特征: 一次函数y=kx+b的图像是经过点(0,b)的直线;正比例函数y=kx的图像是经过原点(0,0)的直线 4、正比例函数的性质 一般地,正比例函数y=kx有下列性质: (1)当k>0时,图像经过第一、三象限,y随x的增大而增大; (2)当k<0时,图像经过第二、四象限,y随x的增大而减小。 5、一次函数的性质 一般地,一次函数y=kx+b有下列性质: (1)当k>0时,y随x的增大而增大 (2)当k<0时,y随x的增大而减小 6、正比例函数和一次函数解析式的确定 确定一个正比例函数,就是要确定正比例函数定义式y=kx(k≠0)中的常数k。确定一个一次函数,需要确定一次函数定义式y=kx+b(k≠0)中的常数k和b。解这类问题的一般方法是待定系数法。 7、一次函数与一元一次方程的关系: 而一次函数解析式形式正是y=kx+b(k、b为常数,k≠0).当函数值为0时,•即kx+b=0就与一元一次方程完全相同. 结论:由于任何一元一次方程都可转化为kx+b=0(k、b为常数,k≠0)的形式. 所以解一元一次方程可以转化为:当一次函数值为0时,求相应的自变量的值. 从图象上看,这相当于已知直线y=kx+b确定它与x轴交点的横坐标值. |
| 高三: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初三: 语文| 数学| 英语| 物理| 化学| 历史| 道德与法制 |
| 高二: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初二: 语文| 数学| 英语| 物理| 地理| 生物| 历史| 道法 |
| 高一: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初一: 语文| 数学| 英语| 物理| 地理| 生物| 历史| 道法 |
| 小学: 语文| 数学| 英语| 道德与法制| 科学| 试题: 小学| 初中| 中考| 高中| 高考| 作文: 小学| 初中| 高中| 满分| 技巧|素材|英汉词典 |
| 高校: 985/211| 各省市| 港澳台| 国外| 排名| 中考专辑| 高考专辑| 各省中学| 职业考试: 从业资格| 技术技能| 艺术等级| 公务员| 百年党史 |
| 课外: 教育动态| 教育法规| 老师榜| 家长帮| 学生派| 安全说| 古诗古文| 世界名著| 近代文学| 寓言故事| 格言名句| 阅读技巧| 在线许愿祝福 |
 移动版
移动版