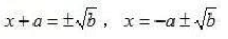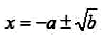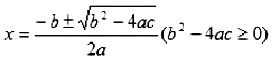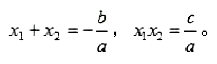【初中数学】BS版九年级上册 第二章 一元二次方程
 2021-10-21
2021-10-21 
 iXueHai.cn
iXueHai.cn
 爱学海
字体 - 小
+ 大 纠错指正
爱学海
字体 - 小
+ 大 纠错指正
|
第二章 一元二次方程 一、一元二次方程 1.一元二次方程定义 含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。 2.一元二次方程的一般形式 ax²+bx+c=0(a≠0),它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中ax²叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 二、一元二次方程的解法 1.直接开平方法 直接开平方法适用于解形如(x+a)²=b的一元二次方程。当b≥0时, 当b<0时,方程没有实数根。 2.配方法 一般步骤: (1)方程ax²+bx+c=0(a≠0)两边同时除以a,将二次项系数化为1。 (2)将所得方程的常数项移到方程的右边。 (3)所得方程的两边都加上一次项系数一半的平方。 (4)配方,化成(x+a)²=b。 (5)开放,当b≥0时, 当b<0时,方程没有实数根。 3.公式法 公式法是用求根公式解一元二次方程的解的方法,它是解一元二次方程的一般方法。 一元二次方程ax²+bx+c=0(a≠0)的求根公式: 4.因式分解法 一元二次方程的一边为0,一边易于分解成两个一次因式的乘积时使用此方法。 三、补充:一元二次方程根的判别式 1.定义:一元二次方程ax²+bx+c=0(a≠0),b²-4ac叫做一元二次方程ax²+bx+c=0(a≠0)的根的判别式。 2.性质:当b²-4ac>0时,方程有两个不相等的实数根;当b²-4ac=0时,方程有两个相等的实数根;当b²-4ac<0时,方程没有实数根。 四、补充:一元二次方程根与系数的关系 如果方程 |
| 高三: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初三: 语文| 数学| 英语| 物理| 化学| 历史| 道德与法制 |
| 高二: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初二: 语文| 数学| 英语| 物理| 地理| 生物| 历史| 道法 |
| 高一: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初一: 语文| 数学| 英语| 物理| 地理| 生物| 历史| 道法 |
| 小学: 语文| 数学| 英语| 道德与法制| 科学| 试题: 小学| 初中| 中考| 高中| 高考| 作文: 小学| 初中| 高中| 满分| 技巧|素材|英汉词典 |
| 高校: 985/211| 各省市| 港澳台| 国外| 排名| 中考专辑| 高考专辑| 各省中学| 职业考试: 从业资格| 技术技能| 艺术等级| 公务员| 百年党史 |
| 课外: 教育动态| 教育法规| 老师榜| 家长帮| 学生派| 安全说| 古诗古文| 世界名著| 近代文学| 寓言故事| 格言名句| 阅读技巧| 在线许愿祝福 |
 移动版
移动版