【物理试题】高一物理必修 第二册 第七章 万有引力与宇宙航行 复习考试题(一)(附答案解析)
 2022-04-02
2022-04-02 
 iXueHai.cn
iXueHai.cn
 爱学海
字体 - 小
+ 大 纠错指正
爱学海
字体 - 小
+ 大 纠错指正
|
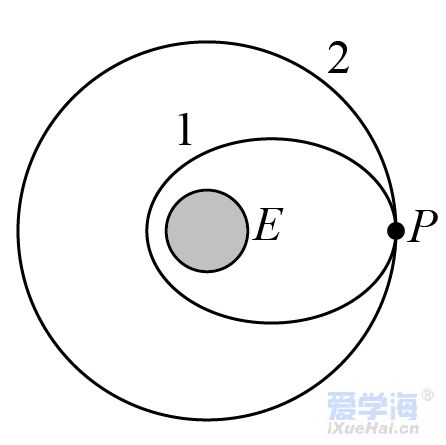
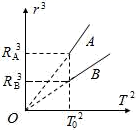
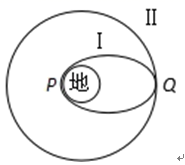
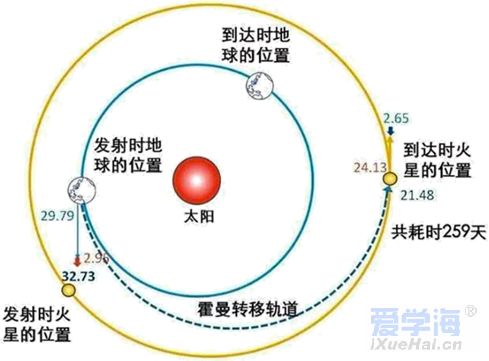
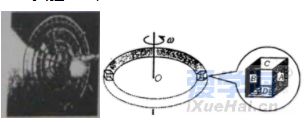
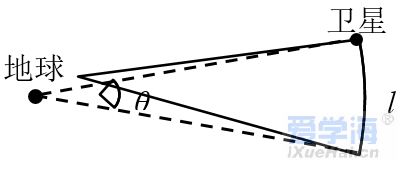
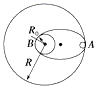
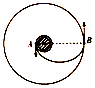
复习考试题(一)(附答案解析) 一、选择题 1.若想检验“使月球绕地球运动的力”与“使苹果落地的力”都遵循同样的规律(即“物体受到地球引力的大小与物体到地球中心距离的平方成反比”),在已知地球表面重力加速度、月地距离和地球半径的情况下,还需要知道( ) A.地球的质量 B.月球的质量 C.月球公转的周期 D.月球的半径 2.如图所示,一颗人造卫星原来在椭圆轨道1绕地球E运行,在P点变轨后进入轨道2做匀速圆周运动。下列说法正确的是( ) A.不论在轨道1还是轨道2运行,卫星在P点的速度都相同 B.不论在轨道1还是轨道2运行,卫星在P点的加速度都相同 C.卫星在轨道1的任何位置都具有相同的加速度 D.卫星在轨道2的任何位置都具有相同的速度 3.2019年1月3日,“嫦娥四号”成为了全人类第一个在月球背面成功实施软着陆的探测器。为了减小凹凸不平的月面可能造成的不利影响,“嫦娥四号”采取了近乎垂直的着陆方式。测得“嫦娥四号”近月环绕周期为T,月球半径为R,引力常量为G,下列说法正确的是( ) A.“嫦娥四号”着陆前的时间内处于失重状态 B.“嫦城四号”着陆前近月环绕月球做圆周运动的速度为7.9km/s C.月球表面的重力加速度g= D.月球的密度为ρ= 4.已知一质量为m的物体分别静止在北极与赤道时对地面的压力差为ΔN,假设地球是质量分布均匀的球体,半径为R。则地球的自转周期为( ) A.T=2π B.T=2π C.T=2π D.T=2π 5.电影《流浪地球》深受观众喜爱,地球最后找到了新的家园,是一颗质量比太阳大一倍的恒星。假设地球绕该恒星做匀速圆周运动,地球中心到这颗恒星中心的距离是地球中心到太阳中心的距离的2倍,则现在地球绕新的恒星与原来绕太阳运动相比,说法正确的是( ) A.线速度大小是原来的2倍 B.角速度大小是原来的2倍 C.周期是原来的2倍 D.向心加速度大小是原来的2倍 6.2020年7月23日12时41分,我国在中国文昌航天发射场,用长征五号遥四运载火箭成功发射首次火星探测任务,“天问一号”探测器,火箭成功将探测器送入预定轨道,开启火星探测之旅,迈出了我国行星探测第一步。已知火星质量与地球质量之比为1:10,火星半径与地球半径之比为,若火星和地球绕太阳的运动均可视为匀速圆周运动,火星公转轨道半径与地球公转轨道半径之比为,下列说法正确的是( ) A.火星探测器的发射速度应介于地球的第一和第二宇宙速度之间 B.火星的第一宇宙速度大于地球的第一宇宙速度 C.火星与地球绕太阳运动的角速度大小之比为 D.火星与地球绕太阳运动的向心加速大小之比为 7.假设宇宙中有两颗相距无限远的行星A和B,自身球体半径分别为RA和RB。两颗行星各自周围的卫星的轨道半径的三次方(r3)与运行公转周期的平方(T2)的关系如图所示,T0为卫星环绕各自行星表面运行的周期。则( ) A.行星A的质量小于行星B的质量 B.行星A的密度小于行星B的密度 C.行星A的第一宇宙速度大于行星B的第一宇宙速度 D.当两行星周围的卫星的运动轨道半径相同时,行星A的卫星的向心加速度小于行星B的卫星的向心加速度 8.如图,在发射地球同步卫星的过程中,卫星首先进入椭圆轨道Ⅰ,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道Ⅱ。则( ) A.该卫星的发射速度必定大于第二宇宙速度11.2km/s B.卫星在同步轨道Ⅱ上的运行速度大于第一宇宙速度7.9km/s C.在轨道Ⅰ上,卫星在P点的速度大于在Q点的速度 D.卫星在Q点通过减速实现由轨道Ⅰ进入轨道Ⅱ 9.某颗中子星的质量为地球质量的a倍,半径为地球半径的b倍,忽略星球自转影响,则该中子星与地球的( ) A.表面重力加速度比值为 B.第一宇宙速度比值为 C.同步卫星轨道半径比值为 D.密度比值为 10.如图所示,O点是近地点,Ⅰ是地球同步卫星轨道,Ⅱ是从地球上发射火星探测器的转移轨道,Ⅲ是火星探测器在近火星点P制动后的圆形轨道,M点是Ⅰ、Ⅱ轨道的交点,则( ) A.火星探测器和地球同步卫星在M点的速度相等 B.火星探测器在P点制动后进入轨道Ⅲ运行时的速度约等于火星的第一宇宙速度 C.火星探测器在O点的速度等于地球的第一宇宙速度 D.火星探测器刚运动到P点时的速度一定等于火星的第一宇宙速度 11.近期世界上掀起了一股火星探测热潮,2020年7月23日12时41分,搭载天问一号的长征五号火箭发射升空,火箭飞行2167秒后探测器与火箭分离。探测器进入地球逃逸轨道(霍曼转移轨道),开启火星探测之旅。以下关于天问一号的火星之旅中说法正确的是( ) A.器箭分离后,探测器靠惯性飞向火星 B.探测器进入霍曼转移轨道后,它的运动不再遵循万有引力定律 C.器箭分离后,探测器进入霍曼转移轨道,在这个轨道内探测器基本只受太阳的引力,则这个过程中它的周期与地球和火星的公转周期的关系为T火>T探>T地 D.“天问一号”被火星“捕获”后,必须加速才能降低轨道高度最后降落在火星表面 12.对于万有引力定律的表述式,下面说法中不正确的是( ) A.公式中G为引力常量,它是由实验测得的,而不是人为规定的 B.当r趋近于零时,万有引力趋于无穷大 C.m1与m2受到的引力总是大小相等的,方向相反,是一对作用力与反作用力 D.m1与m2受到的引力总是大小相等的,而与m1、m2是否相等无关 二、填空题 13.在科幻电影《流浪地球》中,航天器内的字航员们生活在一个匀速转动的圆环形的大管道内,他们具有像生活在地球上一样的重力感觉.如图所示,可简化为半径为r的圆环以角速度绕中心轴O匀速地自转,图中的立方体是空间站内的实验室.则: (1)宇航员日常在实验室的________面上行走;(填:“A”、“B”、“C”或“D”) (2)等效重力加速度“g”与角速度的关系式 _______. 14.如图,某地球卫星在轨道上运动,每经过时间t通过的轨道弧长为l、扫过的圆心角为θ(弧度)。该卫星的周期为________,地球的质量为________。(已知引力常量为G) 15.如图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速周运动,星球A和B两者中心之间距离为L。已知A,B的中心和O三点始终共线,A和B分别O的两侧。引力常数为G。则两星球做圆周运动的周期为_______________,在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期记为。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期.已知地球和月球的质量分别为和。则与两者平方之比为___________________(结果保留3位有效数字) 16.A为地球赤道上的物体,随地球自转的速度为v1,B为近地卫星,在地球表面附近绕地球运行,速度为v2,C为地球同步卫星,距地面高度为地球半径的5倍,绕地球运行的速度为v3,则v1∶v2∶v3=________. 17.某物体在地球表面上受到地球对它的引力大小为960N,为使此物体受到的引力减至60N,物体距地面的高度应为_____R.(R为地球的半径) 18.(1)某一星球的第一宇宙速度为v,质量为m的宇航员在这个星球表面受到的重力为G,由此可知这个星球的半径是________. (2)飞船沿半径为R的圆周绕地球运动,如图所示.其周期为T,如果飞船要返回地面,可在轨道上某一点A处,将速率降低到适当数值,从而使飞船沿着以地心为焦点的椭圆轨道运行,椭圆和地球表面相切于B点,设地球半径为R0,飞船从A点返回到地面上B点所需时间为________. 19.假设在半径为R的某天体上发射一颗该天体的卫星,若它贴近该天体的表面做匀速圆周运动的运行周期为T1,已知引力常量为G,则该天体的密度为________.若这颗卫星距该天体表面的高度为h,测得在该处做圆周运动的周期为T2,则该天体的密度又可表示为________. 20.两行星A和B各有一颗卫星a和b,卫星的圆轨道接近各自行星表面,如果两行星质量之比MA∶MB=2∶1,两行星半径之比RA∶RB=1∶2,则两个卫星周期之比Ta∶Tb=________,向心加速度之比为________. 三、解答题 21.一颗在赤道上空飞行的人造地球卫星,其离地高度为2R(R为地球半径)。已知地球表面重力加速度为g,地球半径为R,万有引力常量为G,求: (1)地球的质量M; (2)该卫星的运行周期T。 22.火星可视为半径为r0的均匀球体,它的一个卫星绕火星运行的圆轨道半径为r,周期为T。求: (1)火星表面的重力加速度; (2)在火星表面离地h处以水平速度v0抛出的物体,落地时速度多大。(不计火星空气阻力) 23.牛顿发现的万有引力定律是17世纪自然科学最伟大的成果之一。万有引力定律在应用中取得了辉煌的成就,应用万有引力定律能“称量”地球质量,也实现了人类的飞天梦想。已知地球的半径为R,地面处的重力加速度为g,引力常量为G,不考虑地球自转的影响。 (1)求地球的质量M; (2)地球同步卫星又称对地静止卫星,其运行角速度与地球的自转角速度ω相同。求该卫星的离地高度h; (3)第2问中该同步卫星的向心加速度大小。 24.卫星发射进入预定轨道时往往需要进行多次轨道调整.如图所示,某次发射任务中先将卫星送至近地圆轨道,然后卫星从圆轨道上A点加速,控制卫星进入椭圆轨道,最后在B点进入距地高为6R的预定圆形高轨道运动,其中A、B分别是两个圆轨道与椭圆轨道相切之处.已知卫星从A点到B点所需的时间为t0,地球半径为R.假定卫星在两个圆轨道上稳定运行时均做匀速圆周运动,求: (1)卫星在高轨道上运行时的周期; (2)地表的重力加速度. 25.我国发射的“嫦娥一号”卫星进入距月球表面高为h的圆轨道绕月运动.设月球半径约为地球半径的,月球质量约为地球质量的,不考虑月球、地球自转的影响,地球表面的重力加速度为g,地球半径为R .求: (1)在月球上要发射一颗环月卫星,最小发射速度v0 (2)“嫦娥一号”卫星在距月球表面高为h的圆轨道上绕月做匀速圆周运动时的速度大小v1 26.万有引力定律揭示了天体运动规律与地上物体运动规律具有内在的一致性。 (1)用弹簧测力计称量一个相对地球静止的小物体的重量,随称量位置的变化可能会有不同的结果。已知地球的质量为M,自转周期为T,万有引力常量为G。将地球视为半径为R、质量均匀分布的球体,不考虑空气的影响。设在地球北极地面称量时,弹簧测力计的读数为F0,若在北极上空高出地面h处称量,弹簧测力计读数为F1,若在赤道地面称量,弹簧测力计读数为F2,求比值的表达式和比值的表达式。 (2)设想地球绕太阳公转的圆周轨道半径r,太阳的半径RS和地球半径R三者均减小为现在的1.0%,而太阳和地球的密度均匀且不变。仅考虑太阳和地球之间的相互作用,以现实地球的1年为标准,计算“设想地球”的一年将变为多长。 【参考答案】 一、选择题 1.C 解析:C 已知地球表面重力加速度g、月地距离r、地球半径R、月球公转的加速度为a,月地检验中只需验证 a = 就可以证明“使月球绕地球运动的力”与“使苹果落地的力”都遵循同样的规律(即“物体受到地球引力的大小与物体到地球中心距离的平方成反比”),而 a = r()2 T为月球公转的周期。要计算月球公转的加速度,就需要知道月球公转的周期。 故选C。 2.B 解析:B A.卫星从轨道1在P点加速才能进入轨道2,则卫星在轨道2上P点的速度大于在轨道1上P点的速度,A错误; B.根据 解得 可知,不论在轨道1还是轨道2运行,卫星在P点的加速度都相同,B正确; C.根据 解得 可知,卫星在轨道1的不同位置具有的加速度不同,C错误; D.卫星在轨道2的任何位置都具有相同大小的速度,但是方向不同,D错误。 故选B。 3.D 解析:D A.在“嫦娥四号”着陆前的时间内“嫦娥四号”需要做减速运动,处于超重状态,故A错误; B.“嫦娥四号”着陆前近月环绕月球做圆周运动的速度不等于地球的第一宇宙速度7.9km/s,故B错误; C.“嫦娥四号”着陆前近月环绕月球做圆周运动时万有引力提供向心力,即 mg=m解得 g=故C错误; D.“嫦娥四号”近月卫星做匀速圆周运动,根据万有引力提供向心力,有 得月球质量 M=又 M=月球的密度 ρ=故D正确。 4.A 解析:A 在北极,物体所受的万有引力与支持力大小相等,在赤道处,物体所受的万有引力与支持力的差值提供其随地球自转的向心力,由题意可得 解得 故选A。 5.C 解析:C A.根据万有引力充当向心力 G=m线速度 v=由题知,新恒星的质量M是太阳的2倍,地球到这颗恒星中心的距离r是地球到太阳中心的距离的2倍,则地球绕新恒星的线速度不变,故A错误; B.根据 可知,线速度不变,半径r变为原来的2倍,角速度大小是原来的倍,选项B错误; C.由周期 T=可知,线速度v不变,半径r变为原来的2倍,则周期变为原来的2倍,故C正确; D.由向心加速度 a=可知,线速度v不变,半径r变为原来的2倍,则向心加速度变为原来的,故D错误。 故选C。 6.C 解析:C A.航天器沿地球表面作圆周运动时必须具备的发射速度,第一宇宙速度,也叫环绕速度;当航天器超过第一宇宙速度达到一定值时,它就会脱离地球的引力场而成为围绕太阳运行的人造行星,这个速度就叫做第二宇宙速度;从地球表面发射航天器,飞出太阳系,到浩瀚的银河系中漫游所需要的最小发射速度,就叫做第三宇宙速度。火星探测器要脱离地球同时不能脱离太阳系,其发射速度应介于地球的第二和第三宇宙速度之间,故A错误; B.近地卫星运行速度近似等于第一宇宙速度,对于地球的近地卫星,有 得 对火星,有 得 故B错误; C.根据得 已知火星公转轨道半径与地球公转轨道半径之比为,则火星与地球绕太阳运动的角速度大小之比为 故C正确; D.根据得 已知火星质量与地球质量之比为,火星公转轨道半径与地球公转轨道半径之比为,火星与地球绕太阳运动的向心加速大小之比为 故D错误。 故选C。 7.C 解析:C A.根据牛顿第二定律有 可得 可知图象的斜率为 由图象可知行星A的斜率大于行星B的斜率,则行星A的质量大于行星B的质量,故A错误; B.密度公式为,行星体积为联立解得 当卫星在行星表面运行时有,r=R,T=T0,则有 由于两卫星绕各自行星表面运行的周期相同,则行星A的密度等于行星B的密度,故B错误; C.行星的近地卫星的线速度即第一宇宙速度,根据牛顿第二定律可得 解得 由于,所以,故C正确; D.根据 可得 由于,两行星周围的卫星的运动轨道半径相同时,行星A的卫星的向心加速度大于行星B的卫星的向心加速度,故D错误。 故选C。 8.C 解析:C A.如果该卫星的发射速度大于第二宇宙速度就离开地球绕太阳运动了,A错误; B.7.9km/s是近地卫星的速度,卫星在圆轨道运动时越高越慢,卫星在同步轨道Ⅱ上的运行速度小于第一宇宙速度7.9km/s; C.由开开普勒第二定律,近地点最快,远地点最慢,卫星在P点的速度大于在Q点的速度,C正确; D.卫星在Q点通过加速做离心运动,实现由轨道Ⅰ进入轨道Ⅱ,D错误。 故选C。 9.A 解析:A A.忽略星球自转影响,在星球表面有 解得 所以它们表面重力加速度比值为,故A正确; B.卫星做圆周运动的向心力由万有引力提供,由向心力公式有 解得 所以第一宇宙速度比值为为,故B错误; C.因为不知道两个星球的自转周期,根据题目所给条件无法求出同步卫星轨道半径比值,故C错误; D.由密度公式得 得密度比值为,故D错误。 故选A。 10.B 解析:B A.火星探测器从M点飞离地球,万有引力不足以提供向心力,地球同步卫星绕地球做圆周运动,则火星探测器和地球同步卫星在M点的速度一定不相等,A项错误; B.火星探测器在P点制动后绕火星做圆周运动,轨道为近火星轨道,故制动后的速度约为火星的第一宇宙速度,B项正确; C.火星探测器经近地点O后做离心运动,可知在O点的速度大于地球的第一宇宙速度,C项错误; D.由题可知,火星探测器在靠近火星阶段的运动轨道不是圆周,需减速做向心运动,所以刚运动到P点时的速度一定大于火星的第一宇宙速度,D项错误。 故选B。 11.C 解析:C A.器箭分离后,探测器飞向火星的过程中,太阳的引力对探测器做负功,则不能只靠惯性飞向火星,选项A错误。 B.探测器进入霍曼转移轨道后,它的运动仍然要遵循万有引力定律,选项B错误; C.器箭分离后,探测器进入霍曼转移轨道,在这个轨道内探测器基本只受太阳的引力,则因火星绕太阳的轨道半径大于探测器绕太阳的轨道的半长轴,大于地球绕太阳的轨道半径,即 r火>a探>r地 根据开普勒第三定律可知 这个过程中它的周期与地球和火星的公转周期的关系为 T火>T探>T地 选项C正确; D.“天问一号”被火星“捕获”后,必须减速才能降低轨道高度最后降落在火星表面,选项D错误。 故选C。 12.B 解析:B A.万有引力定律的表述式中的G为引力常量,它是由实验测得的,不是人为规定的,故A项正确。 B.当物体间间距较小时,物体不能视为质点,万有引力公式不成立。当r趋近于零时,万有引力不会趋于无穷大,故B项错误。 CD.m1与m2受到的引力是一对作用力与反作用力,总是大小相等的,方向相反;与m1、m2是否相等无关.故CD正确. 本题选不正确的,答案是B。 【点睛】 两物体间的万有引力是一对作用力与反作用力,总是大小相等的,方向相反;与两物体质量是否相等无关。 二、填空题 13.B 解析:B (1)[1] 宇航员是靠环对他的支持力提供向心力的,这时宇航员会压紧环,相当于宇航员受到的等效重力方向是背离中心轴O,等效重力的大小等于环对人的支持力,所以宇航员日常在实验室的B面上行走; (2)[2]由上分析可知,等效重力的大小等于环对人的支持力,则有: 等效重力: 所以等效的重力加速度是:. 14. [1]卫星转动的角速度, 则卫星的周期; [2]轨道半径, 根据, 得地球的质量为:。 15.01 解析:01 (1)令A和B圆周运动的半径分别为rA和rB,根据题意有: rA+rB=L ① ② 可得 ③ 将③代入②可得周期 ④ (2)在地月系统中,由于地月系统旋转所围绕的中心O不在地心,由题意知,月球做圆周运动的周期可由下式得出 ⑤ 式中,M和m分别是地球与月球的质量,L是地心与月心之间的距离。若认为月球在地球的引力作用下绕地心做匀速圆周运动,则 ⑥ 式中,T2为月球绕地心运动的周期。由⑥式得: ⑦ 由⑤⑦式得: 代入题给数据得: 16.【分析】同步卫星与随地球自转的物体具有相同的角速度根据v=rω去求线速度之比近地卫星和同步卫星都是绕地球做匀速圆周运动根据万有引力提供向心力去求线速度之比 解析:【分析】 同步卫星与随地球自转的物体具有相同的角速度,根据v=rω去求线速度之比.近地卫星和同步卫星都是绕地球做匀速圆周运动,根据万有引力提供向心力去求线速度之比. 地球赤道上的物体和同步卫星具有相同的周期和角速度,根据v=ωr,地球的半径与同步卫星的轨道半径比为1∶6,所以v1:v3=1∶6;近地卫星和同步卫星都是绕地球做匀速圆周运动,根据万有引力提供向心力,解得v=.两卫星的轨道半径比为1∶6,所以v2∶v3=∶1,所以v1∶v2∶v3=1∶6∶6. 【点睛】 解决本题的关键知道同步卫星与随地球自转的物体具有相同的角速度,以及知道近地卫星和同步卫星都是绕地球做匀速圆周运动,根据万有引力提供向心力可求出线速度之比. 17.3【解析】【分析】根据万有引力定律的内容(万有引力是与质量乘积成正比与距离的平方成反比)解决问题; 解析:3 【解析】 【分析】 根据万有引力定律的内容(万有引力是与质量乘积成正比,与距离的平方成反比)解决问题; 根据万有引力定律表达式得:,其中r为物体到地球中心的距离,某物体在地球表面,受到地球的万有引力为,此时,若此物体受到的引力减小为,根据,得出此时物体到地球中心的距离,所以物体距地面的高度应为. 【点睛】 要注意万有引力定律表达式里的r为物体到地球中心的距离,要求同学们在平时学习过程中加强训练. 18.【解析】 解析: 【解析】 (1)质量为m的宇航员在这个星球表面受到的重力为G,所以星球表面的重力加速度,根据万有引力提供向心力:,可得第一宇宙速度为:,在星球表面根据万有引力等于重力:,联立可得星球半径. (2)根据题意得椭圆轨道的半长轴为:,根据开普勒第三定律得:,解得:,则飞船由A点到B点的运动时间为:. 19. [1].根据万有引力提供向心力 得天体的质量 则天体的密度 [2].若这颗卫星距该天体的表面的高度为h,测得在该处做圆周运动的周期为T2,根据 天体的质量. 则天体的密度 ρ′=. 【点睛】解决本题的关键掌握万有引力提供向心力这一理论列出表达式,结合轨道半径和周期求解中心天体的质量. 20.1:48∶1【解析】卫星做圆周运动时万有引力提供圆周运动的向心力有:得(M是行星的质量R是卫星的轨道半径)故;由得故【点睛】根据万有引力提供向心力列出方程得到周期之比和半径以及质量之间的关系代入数据 解析:1:4 8∶1 【解析】卫星做圆周运动时,万有引力提供圆周运动的向心力,有:,得(M是行星的质量,R是卫星的轨道半径),故;由,得,故. 【点睛】根据万有引力提供向心力列出方程,得到周期之比和半径以及质量之间的关系,代入数据可得结论. 三、解答题 21.(1);(2)(1)不考虑地球自转的影响,地面上质量为m的物体所受重力等于地球对物体引力有 解得 (2)对卫星运用万有引力定律和牛顿运动定律可得 在地球物体 联立解得 22.(1);(2)(1)根据公式 解得 在火星表面 解得 (2)在火星表面离地h处以水平速度v0抛出的物体,落地时竖直方向的速度为 落地时的速度为 23.(1) ;(2) ; (3) (1)在地球表面附近,有 解得 (2)对于同步卫星,有 解得 (3)根据牛顿第二定律得 解得 24.(1)(2)【解析】 (1)当卫星在椭圆轨道上运行时,其半长轴为:由开普勒第三定律有:而卫星从A到B的时间为:故:; (2)卫星在高轨道上有:物体m'在地球表面有:得:点睛:本题需要注意开普勒第三定律的应用,注意找到半长轴,从而求出高轨道的周期,然后在利用:万有引力等于重力、及万有引力等于向心力规律进行求解即可. 25.(1) 26.(1),;(2)1年 (1)设小物体质量为m,在北极地面 在北极上空高出地面h处 在赤道地面,小物体随地球自转做匀速圆周运动,受到万有引力和弹簧秤的作用力,有 得 (2)地球绕太阳做匀速圆周运动,受太阳得万有引力。设太阳得质量为,地球得质量为M,地球公转周期为TE,有: 解得 其中为太阳得密度。由上式可知,地球公转周期TE仅与太阳得密度、地球公转轨道半径与太阳半径之比有关。因此“设想地球”的1年与现实地球的1年时间相同。 |
- 【物理试题】高一物理必修 第二册 第八章 机械能守恒定律 复习考..
- 【物理试题】高一物理必修 第二册 第八章 机械能守恒定律 复习考..
- 【物理试题】高一物理必修 第二册 第八章 机械能守恒定律 复习考..
- 【物理试题】高一物理必修 第二册 第八章 机械能守恒定律 复习考..
- 【物理试题】高一物理必修 第二册 第八章 机械能守恒定律 复习考..
- 【物理试题】高一物理必修 第二册 第七章 万有引力与宇宙航行 复..
- 【物理试题】高一物理必修 第二册 第七章 万有引力与宇宙航行 复..
- 【物理试题】高一物理必修 第二册 第七章 万有引力与宇宙航行 复..
- 【物理试题】高一物理必修 第二册 第六章 圆周运动 复习考试题(..
- 【物理试题】高一物理必修 第二册 第六章 圆周运动 复习考试题(..
- 高一物理第一学期教学质量监测试卷(五)
- 高一物理第一学期教学质量监测试卷(一)
- 【物理试题】高一物理必修 第二册 第八章 机械能守恒定律 复习考..
- 【物理试题】高一物理必修 第二册 第七章 万有引力与宇宙航行 复..
- 【物理试题】高一物理必修 第二册 第六章 圆周运动 复习考试题(..
- 【物理试题】高一物理必修 第二册 第五章 抛体运动 复习考试题(..
- 高一物理第一学期教学质量监测试卷(五)参考答案及解析
- 高一物理第一学期教学质量监测试卷(三)参考答案及解析
- 高一物理第一学期教学质量监测试卷(一)参考答案及解析
- 【物理试题】高一物理必修 第二册 第八章 机械能守恒定律 复习考..
| 高三: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初三: 语文| 数学| 英语| 物理| 化学| 历史| 道德与法制 |
| 高二: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初二: 语文| 数学| 英语| 物理| 地理| 生物| 历史| 道法 |
| 高一: 语文| 数学| 英语| 物理| 化学| 地理| 生物| 历史| 思想政治| 信息技术| 初一: 语文| 数学| 英语| 物理| 地理| 生物| 历史| 道法 |
| 小学: 语文| 数学| 英语| 道德与法制| 科学| 试题: 小学| 初中| 中考| 高中| 高考| 作文: 小学| 初中| 高中| 满分| 技巧|素材|英汉词典 |
| 高校: 985/211| 各省市| 港澳台| 国外| 排名| 中考专辑| 高考专辑| 各省中学| 职业考试: 从业资格| 技术技能| 艺术等级| 公务员| 百年党史 |
| 课外: 教育动态| 教育法规| 老师榜| 家长帮| 学生派| 安全说| 古诗古文| 世界名著| 近代文学| 寓言故事| 格言名句| 阅读技巧| 在线许愿祝福 |
 移动版
移动版